1. viikko (16.—20. maaliskuuta)

Ohjeet kotitöihin ekalle viikolle. Lyhyemmät ohjeet ilmestyvät myös Wilmaan ennen kutakin tuntia.

Palautukset peda.net-palveluun jollei ole muuta mainittu.

7. luokka

Matematiikka

Opiskele normaaliin tapaan viimeiset kappaleet kirjasta. Uusia asioita ei enää tule, mutta kertausta. Muista, että tarkistan tekemäsi tehtävät. Eli

Apua saa ja pitää kysyä. Ylhäällä ohjeet avun saamiseksi.

Koe

Matematiikan koe aihepiiristä on torstaina 19.3. Kokeet ilmestyivät tähän keskiviikkoiltana ja se palauttaa kuvana viimeistään torstai-iltana Discordiin tai sähköpostitse. Saat käyttää siis käyttää kaikkea materiaalia apuna, myös Photomathia ja huoltajia tai paikallista matikan proffaa. Mutta, kirjoita välivaiheet näkyviin. Muista siis tarkistaa. Tee hyvää työtä. Kaikkien kokeet ovat erilaiset, joten suora kopiointi ei onnistu. Kirjoita käsin, omalla käsialalla.

Fysiikka

Lue seuraava kappale kirjasta eli kpl 2 (oli muuten jo kotiläksynä) ja tee sekä kirjan että työkirjan tehtävät. Kysy apua.

Käytiin kappale 3, onko muuten kappaleen kaksi tehtävät vielä tekemättä? Palauta työkirjan tehtävistä s 18-19 kuva peda.netiin.

Kotitehtävinä lukukirjasta s 21 teht 23, 25 ja 27.

Maantieto

Etsi Tallinnan lähialueilta eroosion eli lähinnä veden ja tuulen aiheuttamia jälkiä. Ota kuva ja palauta se tähän palautuskansioon. Ota ainakin kolme kuvaa samasta aiheesta eri kuvakulmista ja zoomauksella. Palautus peda.net kappaleeseen 8 tehtäviin. Siellä se odottelee ensimmäisenä. Arviointi:

8. luokka

Matematiikka

Suunnitelman mukaan:

  • Ti: kappale 11: muuttujan arvon laskeminen
  • Ke: kappale 13: kertaus alkuun
  • To: kappale 13: kertaus loppuun

Fysiikka

Lue seuraava kappale kirjasta eli kpl 16 Energia muuntuu muodosta toiseen (oli muuten jo kotiläksynä) ja tee sekä kirjan että työkirjan tehtävät. Kysy apua. Katso videt

Huom, kaikkea ei kuulu tehdä maanantaina, mutta perjantaiksi tulee hieman lisää.

Perjantain laskut. Eli ruvetaan heti laskemaan energiaa. Meille tulee noin kolme käsitettä työ, kineettinen energia ja potentiaalienergia. Viimeisin oli mielestäni hankala ymmärtää, koska nollakohdan saat valita ihan itse.

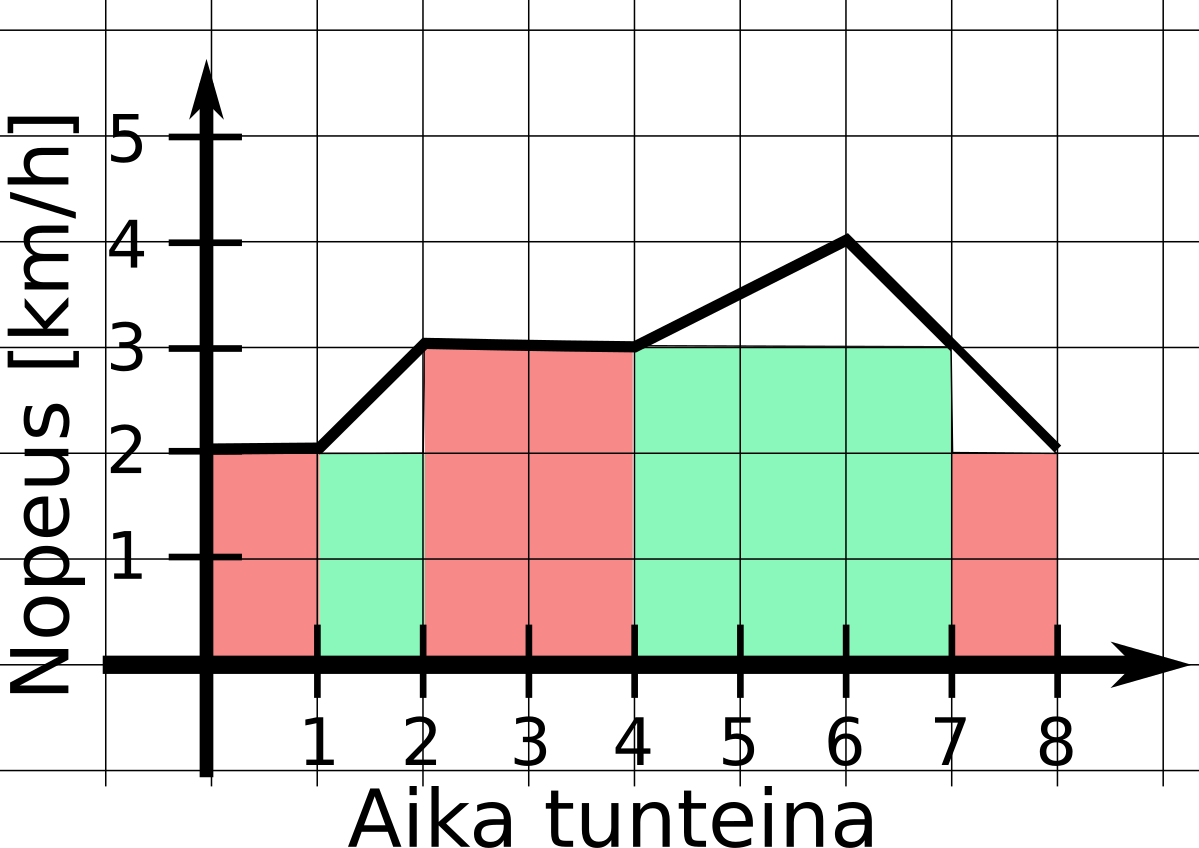
Kertaus nopeudesta. Koska nopeus on matka jaettuna ajalla, niin matka on nopeus kertaa aika; eli s = vt. Mutta tässä me huijataan aina. Nyt ei huijata, vaan lasketaan oikein. Oikeasti matka on vt-kuvaajan alle jäävä pinta-ala. eli

Kuvaajassa näkyy nopeus (v) ja aika (t). Matka voidaan helposti laskea ensimmäiselle punaiselle suorakaiteelle, koska matka s = vt, eli s1 = 2×1. Seuraava aikaväli koostuu kahdesta osasta, vihreästä suorakaiteesta ja valkoisesta kolmiosta. Mutta niidenkin pinta-ala osataan laskea: s2 = 2×1 + 1×1/2 = 2,5 koska siis kolmion pinta-ala.

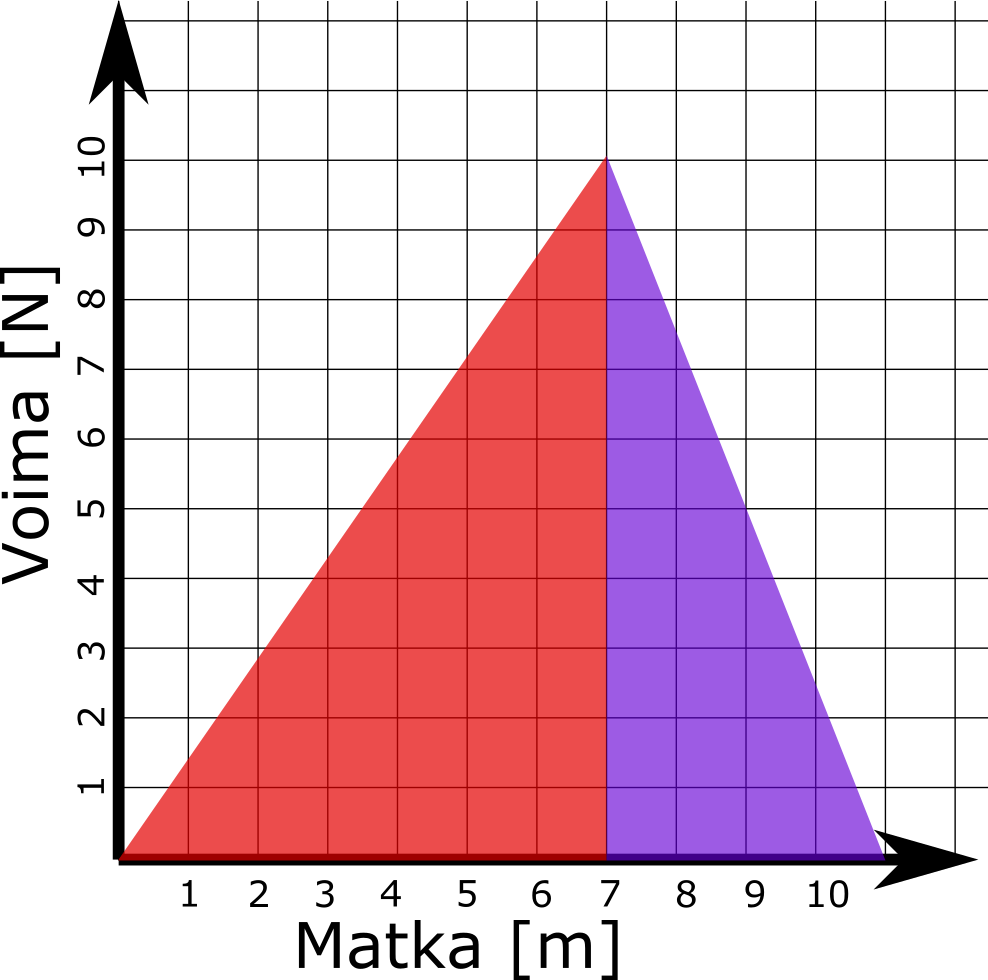
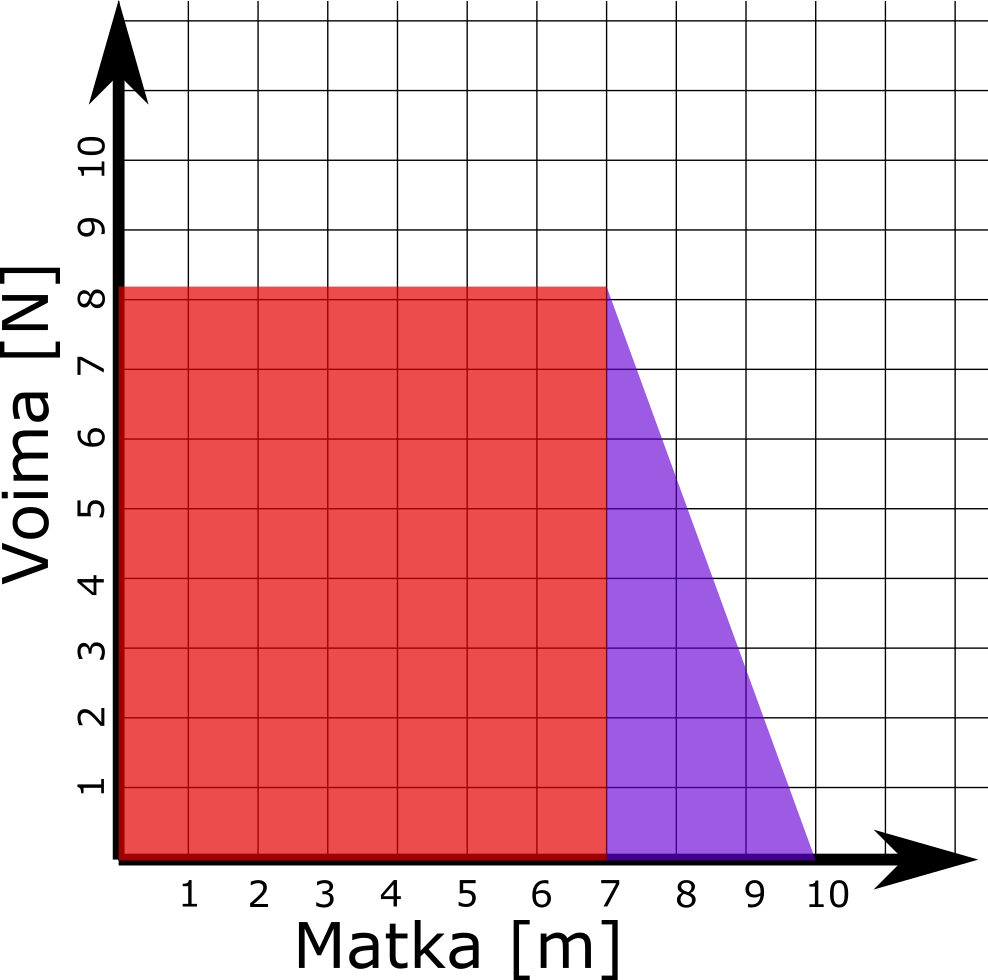
Tehtävä Laske matka, jonka kuvaajassa oleva härpäke kulki.

Sama juttu on kaikilla fysiikassa esiintyvillä kertolaskuilla. Siis, vielä muutama harjoitustehtävä.

Tehtävä Laske työ (Work, W), jonka kuvaajassa oleva härpäke kokee. W = Fs

Tehtävä Laske työ (Work, W), jonka kuvaajassa oleva härpäke kokee. W = Fs

Maantieto

Tehtävä 1

Keskitorilla ja muuallakin on jo myynnissä kreikkalaisia mansikoita.

  • Selvitä netistä, koska Kreikassa mansikat kypsyvät.
  • Lisäksi etsi kuva kreikkalaisesta mansikkamaasta.
  • Vielä, piirrä vihkoosi Euroopan kartta ja siihen mansikoiden oletettu reitti Kreikasta Tallinnaan. Minkä kaupunkien kautta se kulkee? Mitä teitä pitkin? Käytä vaikka Open Street Mappia apuna
Tehtävä 2

Tutki Flight Radar 24 -palvelusta (saattaa olla laiton Suomessa) miten, mistä ja ja minne lentokoneita lentää. Vastaa vihkoosi seuraaviin kysymyksiin:

  • Kirjoita kymmenen (10) kaupunkia joiden lähistöllä on paljon lentokoneita
  • Onko Suomessa paljon lentoliikennettä?
Tehtävä 3

Avaa Marine Vessel Trafic -palvelu ja selvitä vihkoosi

  • Mitä muita aluksia Suomen ja Viron välillä kulkee kuin ne matkustajalautat?
  • Mistä ne ovat tulossa?
  • Mistä maista tulee kymmenen Suomenee tulevaa laivaa?
  • Missä päin on suurimmat laivaliikennekeskittymät
  • Tutki kanavien Suez ja Panama vaikutusta meriliikenteesen. Kuinka monta laivaa kulkee näissä kanavissa? Entä odottamassa kanavaan pääsyä?
Tehtävä 4 (lisätty 17.3.2020)

Lue Iltasanomain juttu Schengen alueesta Korona tappaa Euroopan unelman.

Tehtävä 5 (lisätty 17.3.2020)

Katso ja tutki karttaa maailman valtioista tiheyden mukaan.

9. luokka

Matematiikka

Suunnitelman mukaan.

Maanantaina pallon pinta-ala loppuun

Tiistaina pallon tilavuus ja keskiviikkona pallon tilavuus loppuun.

Keskiviikkona siis pallon tilavuus loppuun.

Torstaina viimeistelypäivä. Koe pidetään koulussa, jos päästään sinne lähiaikoina, muutoin koe pidetään kotokokeena. Silloin kaikki materiaali on käytettävissä.

Kemia (ja fysiikka)

Posteri englanninkielellä Inkscapella tehtynä. Jollei ole tietokonetta käytettävissä, saat käyttää erikoisluvallamyös esim. Googlen ohjelmistoja. Tarkoituksena on oppia samalla Inkscapea.

Inkscape on äärimmäisen hieno ohjelma, mutta hieman hankala etäyhteyksien kanssa. Siispä, voitte käyttää muitakin hyviä menetelmiä, mutta ongelmaksi muodostuu helposti Googlesta riippuvaisuus.

Millainen posteri? Tällä kertaa posteri tehdään Mendelevin jaksollisen järjestelmän pohjalta alkuaineiden mukaan!

  • Muuta otsikko: Biologin ->
  • Älä muuta keskellä isolla olevaa jaksollista järjestelmää
  • Oikealla oleva "Orgaaniset yhdisteet sisältävät. . . " muutat oman aiheesi mukaiseksi, esim. "Raakaöljyn tislauksessa. . ." ja lisäät sinne sopivia kuvia, joko molekyyleistä tai prosesseista.
  • Sen alla on laatikko tekijöistä. Laittakaa sinne omat tiedot.
  • Alla keskellä oikealla olevaan "Kondensaatioreaktio" -laatikkoon laitat esim. "Tekstiilikuitujen valmistus saastuttaa ympäristöä"
  • Alhaalla vasemmalla oleva iso alkuainelaatikko, jonka saat tehdä uudestaan oman aiheesi mukaan.
  • Tekstit tietenkin englanniksi!
  • Toinen laatikko molekyyleille, toinen prosesseille.

Koita säilyttää sama tyyli.

Ohjeet löytyvä myös youtubesta

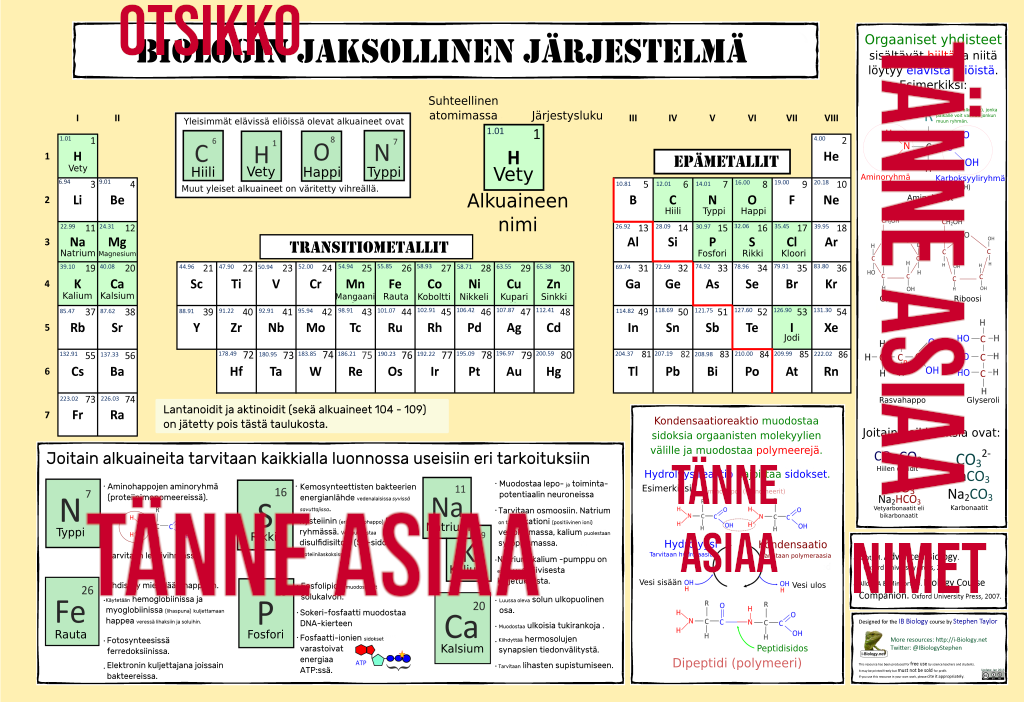
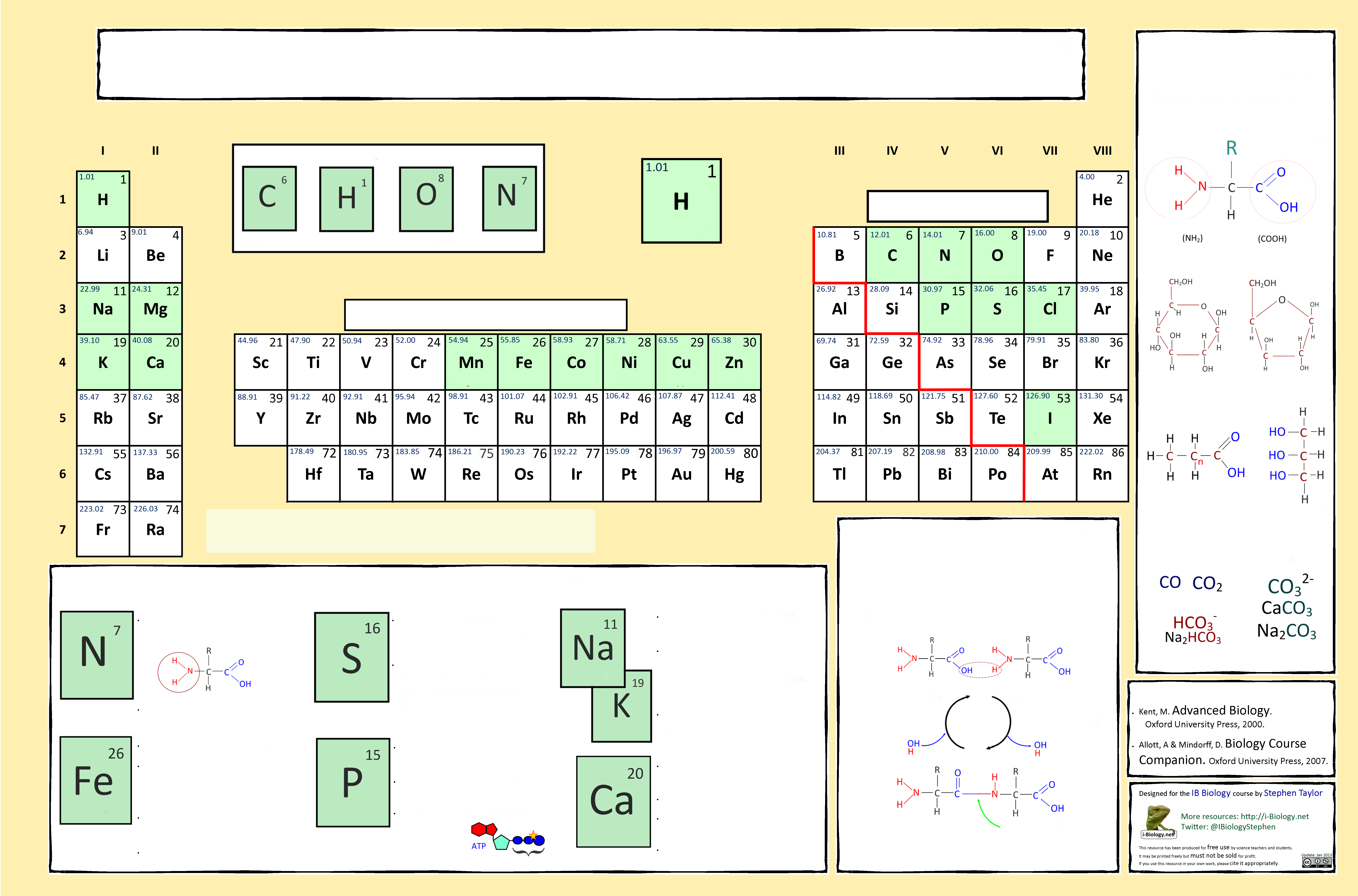
Lataa inkscapella editoitava versio tästä. Mulla se avaa Chromen uuteen ruutuun, mutta sieltä voit tallettaa sen Save as tai jotain vastaavaa. Editoi tätä tiedostoa.

Torstai 19.3. valitset parin tai pienen kolmen hengen ryhmän, ja keksitte aiheen, aloitatte työn ja lähetät ensimmäisen version minulle. Aiheita on mm.

  • Fossiiliset polttoaineet (kirja s 166)
  • Muovit (kirja s 168)
  • Testiilikuidut (kirja s 170)
  • Puu ja paperi (kirja s 172)
  • Pesuaineet (kirja s 174)
  • Lääkkeet (kirja s 176)
  • Rasvat (kirja s 154)
  • Meni jo: Sokerit (kirja s 158)
  • Proteiinit (kirja s 162)
  • Meni jo: Sokerit??
  • Muu mielenkiintoinen aihe — esimerkiksi ne tappavat alkuaineet.
  • Tai ruoanlaiton kemiaa: nostatusaineet, hiivat, sidosaineet, sitko jne.
  • Tai pigmentit, väriaineet, -molekyylit tai maali. Esim. okra, titaanivalkoinen, rautaoksidi, lyijyvalkoinen, umbra, mikäs siinä videossa oli.

Torstai 26.3. Viimeistely, palautus. Ohjeita saa, tietenkin.

Maantieto

Käsityötä, eli piirrä käsin paperille. Jokainen omansa. Iso työ, mutta jos jotain jää päähän, niin helpottaa. Tässä on koko kahden viikon työt. Palauta ensimmäisellä viikolla kuva alkuosasta ja ensi viikolla loppuosa. Merkitsen Wilmaan ne tehdyt työt.

Suomen maantieto jatkuu saman kartan päälle, jota aloitettiin perjantaina koulussa. Jos hukkasit kartan, voit piirtää isolle paperille (mielellään A3-kokoa, eli ison vihon aukeama) Suomen reunaviivat. Lisää siihen seuraavat asiat. Huom tee vesistöt sinisellä.

Ennen vuotta 1600 perustetut kaupungit ja läheiset vesistöt:

  • Turku ja Aurajoki
  • Ulvila ja Kokemäenjoki
  • Porvoo ja Porvoonjoki
  • Rauma ja sen läheinen Pyhäjärvi
  • Naantali ja piirrä sen ympäristölle Turun ja Paraisten saaristoa. Muista Jurmo ja Utö.
  • Tammisaari sen saaristo.
  • Helsinki ja Suomenlinna, Vantaanjoki
  • Pori, Kokemäenjoki tuli jo

Ennen vuotta 1700 perustetut kaupungit:

  • Oulu ja Oulujoki sekä Oulujärvi. Lisää myös Kajaani, Vuokatti ja Sotkamo.
  • Vaasa. Piirrä myös Vaasan saaristo, Laihia, Seinäjoki ja Mustasaari.
  • Uusikaupunki ja sen saaristo.
  • Kokkola ja Kalajoki (joka ei ole joki)
  • Uusikaarlepyy ja Uusikaarlepyyn joki sekä Lappajärvi.
  • Tornio ja Tornionjoki
  • Hämeenlinna ja Vanajvesi, Iso-Roine, Hiidenjoki,
  • Savonlinna ja Pieni Haukivesi, Puruvesi, Saimaa ja Rääkkylä
  • Lappeenranta ja Nuijamaa
  • Raahe ja Hailuoto
  • Kristiinankaupunki sekä Söderfjärden
  • Kajaani tuli jo, mutta lisää Pielinen
  • Kuopio ja Kallavesi ja Konnevesi
  • Pietarsaari
  • Hamina ja Kotka. Lisää myös Kymijoki ja Pyhäjärvi, josta se laskee.

Ennen vuotta 1800 perustetut kaupungit

  • Loviisa ja saaristoo Porvooseen ja Kotkaan saakka.
  • Tampere ja Näsijärvi ja Pyhäjärvi. Jatka Kuloveden kautta Rautavdelle ja siitä Kokemäenjokeen. Etelään yhdistä Pyhäjärvi Vanajaveteen. Pohjoiseen piirrä järviä Tampereen pohjoispuolella, ja merkitse karttaan myös Teisko, Murole, Ruovesi, Vilppula, Keuruu, Virrat ja Mänttä. Itään päin merkitse Kangasala, Roine, Längelmävesi, Päijänne ja Jyväskylä
  • Kaskinen sekä piirrä sen saaristoa. Erityisesti pohdi, miksi se on sen näköistä.

    • Ennen vuotta 1900 perustetut kaupungit

    • Jyväskylä ja Konnevesi sekä Keitele
    • Mikkeli
    • Heinola ja Päijänne
    • Joensuu ja Koli sekä Pielinen
    • Maarianhamina ja saaret Föglö, Sottunga, Kumlinge, Kökar ja Houtskär
    • Kemi ja Kemijoki sekä Kemijärvi
    • Hanko ja Rosala, Bengtskär ja Russarö
    • Kotka
    • Iisalmi, Porovesi ja Iso-Ii

    Sekä

    • Lahti, Suomen Chicago

    Luettelo Suomen kaupungeista perustamisvuoden mukaan

    Eikä tässä vielä kaikki. Lisäksi tarvitaan Suomen suurimmat järvet järjestyksessä. Huomaa, että osa tuli jo äsken.

    • Saimaa (mm. Etelä-Saimaa, Pihlajavesi, Haukivesi, Pyhäselkä, Puruvesi, Luonteri ja Kolovesi)
    • Päijänne
    • Inarijärvi
    • Iso-Kalla (Kallavesi, Suvasvesi, Juurusvesi, Riistavesi ja Muuruvesi)
    • Pielinen
    • Oulujärvi
    • Keitele
    • Kallavesi
    • Puula
    • Lokan tekojärvi
    • Kitkajärvi (Yli-Kitka ja Ala-Kitka) ja Posiojärvi
    • Längelmävesi, Koljonselkä ja Roine – Mallasvesi
    • Iisvesi, Niinivesi, Rasvanki ja Virmasvesi.
    • Iso-Kulovesi (Kulovesi, Rautavesi)
    • Höytiäinen
    • Näsijärvi

    Luettelo Suomen (sisä)vesistöistä.

    Ja vielä. Sitten tarvitaan Suomen joet pohjoisesta lounaan kautta itään.

    Lue joista hyvä teksti Pääjoet. Lisää karttaasi seuraavat joet

    • Oulujoki
    • Siikajoki
    • Pyhäjoki
    • Kalajoki
    • Lestijoki
    • Perhonjoki
    • Ähtävänjoki
    • Lapuanjoki
    • Kyrönjoki
    • Närpiönjoki
    • Isojoki
    • Merikarvianjoki
    • Pohjajoki
    • Eteläjoki
    • Kellahdenjoki
    • Kokemäenjoki
    • Eurajoki
    • Lapinjoki
    • Ilmonhauta
    • Mynäjoki
    • Hirvijoki
    • Aurajoki
    • Paimionjoki
    • Uskelanjoki
    • Vantaanjoki
    • Sipoonjoki
    • Mustijoki
    • Porvoonjoki
    • Ilolanjoki
    • Loviisanjoki
    • Lillån
    • Kymijoki
    • Summanjoki
    • Vehkajoki
    • Huh, se oli siis kahden viikon tehtävä.

    Paitsi, että saat vielä lukea Pedasta kappaleen 10. Kartat.

    Fysiikka: Ekstratehtävät

    Energia ja yhteiskunta -kurssi

    Tiistaina 17.3. aloitetaan riskianalyysi helpolla esimerkillä:

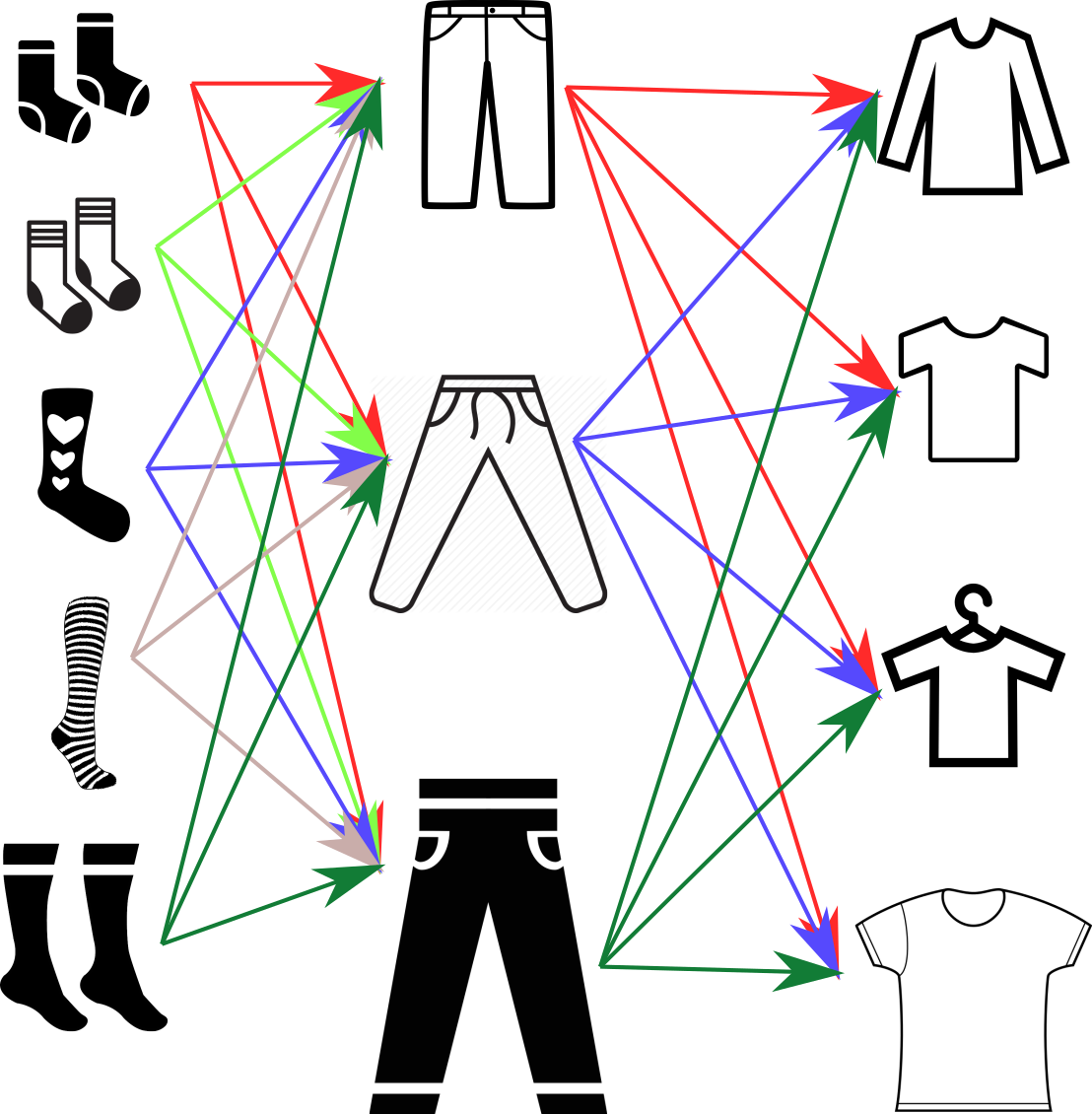
    Esimerkki: Sinulla on viidet eriväriset sukat, kolmet housut ja neljä paitaa jotka kaikki sopisivat päivän teemaan. Kuinka monta erilaista asuvaihtoehtoa näistä saat?

    Kuvassa näkyy vaatteet ja eri vaihtoehdot. Kaikkiaan, kun lasket kaikki nuolet huomaat, että nuolia on 5×3×4 = 60 eri vaihtoehtoa.

    Todennäköisyys valita jokin noista on siis 1/60. Eli 60 päivänä voit pitää eri vaatekertaa, sen jälkeen tulee pakosta toistoa.

    Tehtävä 1. Kuusi kaverusta tilaa ja hakee pizzan, mutta vain kolmella on puhelin ja neljällä ajokortti. Siis kuinka monta eri vaihtoehtoa on

    • soittajalle?
    • kuskille?
    • kuka kävelee autosta pizzeriaan?
    Mikä on kokonaisvaihtoehtojen määrä?

    Tehtävä 2. Katso video Art of Problem Solving: Counting with Combinations Part 1

    Tehtävä 3. Ysiluokalta (14 oppilasta) valittiin puheenjohtaja täysin satunnaisesti. Mikä on todennäköisyys, että nimi tulee valituksi?

    Tehtävä 4. Katso video Art of Problem Solving: Permutations and Factorials

    Tehtävä 5.Neljätoista (14) ysiluokkalaista laitetaan siistiin jonoon. Kuinka monta erilaista jonoa on olemassa?

    Tehtävä 6. pussissa on keltainen, punainen ja sininen pallo. Jos ensimmäisenä nostetaan punainen pallo, niin jäljelle jää vain kaksi vaihtoehtoa. Seuraavan pallon jälkeen vaihtoehtoja on enää yksi. Erilaisten nostojärjestysten lukumäärä on siis

    Tehtävä 7. Millä todennäköisyydellä nopan tulos on 2?

    Tehtävä 8. Millä todennäköisyydellä kolmea noppaa heitettäessä saadaan vähintään yksi kutonen

    • Laske ensin, todennäköisyys että saadaan yksi kuutonen
    • Yhdistä tuloksesi kolmelle nopalle TAI-eli + -operaattorilla

    Tehtävä 9. Millä todennäköisyydellä kolmea noppaa heitettäessä saadaan tasan yksi kutonen

    • Laske ensin, todennäköisyys että saadaan yksi kuutonen
    • Yhdistä tuloksesi kolmelle nopalle JA-eli × -operaattorilla

    Tehtävä 10 Koulumatkalla on kolmet liikennevalot (jalankulkijoille). Jokaisessa liikennevalossa on punainen ja vihreä valo. Mikä on todennäköisyys sille, että joudut pysähtymään kaikissa valoissa? Vihje: Kirjoita kaikki vaihtoehdot näkyviin; esim EEE, EEK, EKE jne. Kuinka monta niitä on yhteensä?

    Tehtävä 11 Koulumatkalla on kolmet liikennevalot (jalankulkijoille). Jokaisessa liikennevalossa on punainen ja vihreä valo. Mikä on todennäköisyys sille, että et joudu pysähtymään kertaakaan? Vihje: Sama kuin edellä

    Tehtävä 12 Koulumatkalla on kolmet liikennevalot (jalankulkijoille). Jokaisessa liikennevalossa on punainen ja vihreä valo. Mikä on todennäköisyys sille, että joudut pysähtymään tasan kerran? Vihje: Sama kuin edellä

    Tehtävä 13 Koulumatkalla on kolmet liikennevalot (jalankulkijoille). Jokaisessa liikennevalossa on punainen ja vihreä valo. Mikä on todennäköisyys sille, että joudut pysähtymään ainakin kerran? Vihje: Sama kuin edellä